Coloured tinkerbell fractal with generativepy

By Martin McBride, 2021-06-06

Tags: tinkerbell fractal
Categories: generativepy generative art

This article has been moved to my blog. Please refer to that article as it might be more up to date.

We created a Tinkerbell fractal in the previous article, but it was a black and white version. In this section we will look at how to create a full colour version like this:

Where does the colour come from?

Our black and white version starts with a white background, then as the algorithm runs, each time it lands on a pixel that pixel is set to black. It therefore creates an image of every pixel the algorithm has visited.

The algorithm often lands on the same pixel more than once. In this chapter we will employ a slightly different technique. We will keep a counter for every pixel, that starts at zero and gets increment by 1 each time the algorithm lands on it. We can then give each pixel a colour based on its count. In this case we will use a black background and assign lighter colours to the pixels. The bigger the count, the lighter the pixel.

Code changes

We will modify the previous code in two ways:

The original loop will be modified to count the number of hits on each pixel.
A second stage is used to apply colour to the pixels.

Here is the code the paint part of the code

def paint(image, pixel_width, pixel_height, frame_no, frame_count):
    scaler = Scaler(pixel_width, pixel_height, width=3, startx=-2, starty=-2)

    x = 0.01
    y = 0.01
    for i in range(MAX_COUNT):
        x, y = x*x - y*y + A*x + B*y, 2*x*y + C*x + D*y
        px, py = scaler.user_to_device(x, y)
        image[py, px] += 1

data = make_nparray_data(paint, 600, 600, channels=1)
save_nparray("/tmp/temp.dat", data)

This time the paint function works in a similar way to before, but instead of setting the pixel to zero, it increments the value in image[py, px].

Notice also that we are using make_nparray_data to create the array. This function doesn't create an image, instead it returns the NumPy arrays itself. Also, it initialises the array to 0 rather than 255.

The end result of this stage is an array of the counts of the number of times each pixel has been visited. This data is saved as temp.dat. That is a data file containing the NumPy data, it isn't an image file.

Colorising

Next is the colorising code:

def colorise(counts):
    counts = np.reshape(counts, (counts.shape[0], counts.shape[1]))
    power_counts = np.power(counts, 0.25)
    maxcount = np.max(power_counts)
    normalised_counts = (power_counts * 1023 / max(maxcount, 1)).astype(np.uint32)

    colormap = make_npcolormap(1024, [Color('black'), Color('red'), Color('orange'), Color('yellow'), Color('white')])

    outarray = np.zeros((counts.shape[0], counts.shape[1], 3), dtype=np.uint8)
    apply_npcolormap(outarray, normalised_counts, colormap)
    return outarray

data = load_nparray("/tmp/temp.dat")
frame = colorise(data)
save_nparray_image('tinkerbell.png', frame)

This code does the following:

Loads the temp.dat back into a NumPy array (see the note below).
Calls the colorise function to convert the counts (in data) into RGB values (in frame).
Saves the frame as a PNG file.

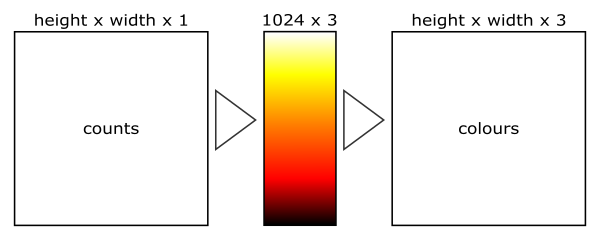
Looking at the code in colorise, step by step it does the following:

Reshape our counts array from (height, width, 1) to (height, width). This doesn't actually affect the array data at all, it is just easier to work with a 2D array of counts.
Raise each count to the power of 0.25, stored as power_counts. This equalises the colours a bit (see below).
Find the maximum count, maxcount.
Normalise the power_counts array to have values in the range 1 to 1023. This gives us 1024 distinct colours, which is enough to give a nice image.
make_npcolormap creates a colour map with 1024 colours (colour values 0 to 1023). The list of colours means that the map will move from black to red to orange to yellow to white as the count increases from 0 to 1023.
Finally we create an output array that is height by width by 3, to hold RGB image data. The array is of type uint8, that is unsigned byte value. We call apply_npcolormap to convert the normalised count array into an RGB image array.

Why write the counts array out to file

You might be wondering why we write the counts array out to the file temp.dat and then read it in again straight away.

The reason is that calculating the counts array takes a while (a few minutes on a typical PC at the time of writing), but colorising is very quick. If you want top experiment with different colours, what is the point of regenerating the counts array again each time?

After running the complete code for the first time, the temp.dat file will already have been created. So you can comment out these two lines of code:

# data = make_nparray_data(paint, 600, 600, channels=1)
# save_nparray("/tmp/temp.dat", data)

If you run the code again with different colours, it won't recalculate the counts array again, so it will go a lot faster!

Why call the power function on the counts array?

You might be wondering why we call np.power on the counts array.

To understand this, we can look at the histogram of values in the counts array, like this:

from generativepy.analytics import print_stats, print_histogram

print_stats(counts[counts>0], title="stats")
print_histogram(counts[counts>0], title="histogram")

These functions are provided by the generativepy analytics module, to allow you to analyse frame data.

We analyse counts[counts>0], which is basically the counts array but ignoring any entries that are zero. We are interested in the distribution of colours, we don't need to worry about the black background pixels that have a count of zero.

print_stats prints:

Min: 1
Max: 36117
Mean: 741.18
Median: 124.0

This shows the range of counts goes from pixels that have a count of just one, right through to pixels that have a count of 36117. That is a huge range, but if you look at the averages they are very low. The median is only 124, which means that hale the pixels are in the range 1 to 124, the othetr half are in the range 125 to 36117. That is quite unbalanced.

print_histogram shows a similar story:

To understand this histogram, the total range of counts (1 to 36117) is dived into 10 equal ranges. So this shows that 12934 pixels had a count in the range 1 to 3611, 260 pixels had a count in the range 3612 to 7223, and so on. It show that almost all of the pixels had vary low counts, with a very small number of pixels having high values.

If we displayed this data as it is, almost all the pixels would be almost black, with a very small number of bright pixels. That would be accurate, but not very exciting to look at.

If we take the 4th root of every value, this makes all the numbers smaller, but it actually has a bigger effect on the larger numbers than the smaller numbers. This has the effect of evening out the range a bit. The stats for power_counts are:

Min: 1.0
Max: 13.785671241421008
Mean: 3.622110633199732
Median: 3.3369939654815144

The mean and median are now around 25% of the maximum (rather than 2% in the case of counts). The histogram is better balanced too:

It isn't perfectly equalised, but that isn't necessarily a bad thing. Sometimes if the very brightest colours don't appear much it can make the highlights more effective. It is all a matter of personal choice.

This isn't the only way of equalising the histogram. You can also use logarithms, or simply fitting the colours to the histogram piecemeal. We will investigate these techniques in a alter article.

Full code

Here is the full code:

from generativepy.bitmap import Scaler
from generativepy.nparray import make_nparray_data, save_nparray, load_nparray, make_npcolormap, apply_npcolormap, save_nparray_image
from generativepy.color import Color
from generativepy.analytics import print_stats, print_histogram
import numpy as np

MAX_COUNT = 10000000
A = 0.9
B = -0.6013
C = 2.0
D = 0.5


def paint(image, pixel_width, pixel_height, frame_no, frame_count):
    scaler = Scaler(pixel_width, pixel_height, width=3, startx=-2, starty=-2)

    x = 0.01
    y = 0.01
    for i in range(MAX_COUNT):
        x, y = x*x - y*y + A*x + B*y, 2*x*y + C*x + D*y
        px, py = scaler.user_to_device(x, y)
        image[py, px] += 1


def colorise(counts):
    counts = np.reshape(counts, (counts.shape[0], counts.shape[1]))
    power_counts = np.power(counts, 0.25)
    maxcount = np.max(power_counts)
    normalised_counts = (power_counts * 1023 / max(maxcount, 1)).astype(np.uint32)

    colormap = make_npcolormap(1024, [Color('black'), Color('red'), Color('orange'), Color('yellow'), Color('white')])

    outarray = np.zeros((counts.shape[0], counts.shape[1], 3), dtype=np.uint8)
    apply_npcolormap(outarray, normalised_counts, colormap)
    return outarray


data = make_nparray_data(paint, 600, 600, channels=1)

save_nparray("/tmp/temp.dat", data)
data = load_nparray("/tmp/temp.dat")

frame = colorise(data)

save_nparray_image('tinkerbell.png', frame)