Tinkerbell fractal with generativepy
Categories: generativepy generative art

This article has been moved to my blog. Please refer to that article as it might be more up to date.
The Tinkerbell fractal is based on an iterated function. Here we will look at an implementation using generativepy.
Here is a simple black and white version of the fractal (the coloured version in the next article is a lot nicer):

Tinkerbell algorithm
The Tinkerbell fractal is based on two simple equations that take a value (x, y) and calculate a new value (xnext, ynext). The formulas are:
xnext = x*x - y*y + A*x + B*y
ynext = 2*x*y + C*x + D*y
Suitable parameters are:
A = 0.9
B = -0.6013
C = 2.0
D = 0.5
x = 0.01 # Initial value
y = 0.01 # Initial value
We start with the initial value (0.1, 0.1). We place a dot on the page at this position.
Next, we feed those values into the equations above, which creates news x and y values (0.002987, 0.0252). We place another dot at that position.
We then feed those new values back into the same equations, which creates news x and y values (-0.013090577831 0.0187245448). We place another dot at that position.
This process is illustrated here:
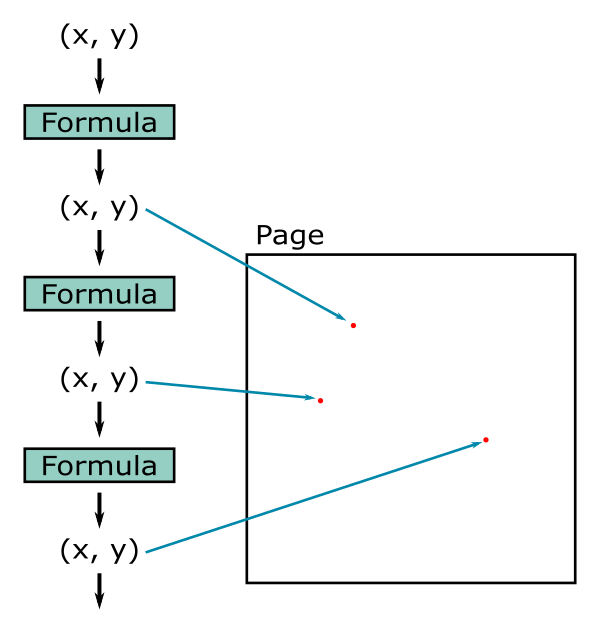
We repeat this procedure many more times. The next few values of x and y are:
-0.023219834186157737 -0.017309113484108886
-0.01025032553952039 -0.05429039562434912
0.020577144019970572 -0.046532860433577475
These positions all seem quite random. However, if you plot thousands of points, a pattern emerges as we saw above. Even though each new pixels seems to be in a random position, in fact all the pixels end up in a particular part of the image. It is as if they all seem to land on a particular, complicated curved shape.
In fact, it is stranger than that. If you look at some of the loops in the curve, you will see that there are actually several separate lines that each follow a similar path. But if we were to zoom in further, we would find that each of those lines is actually made up of several different lines, very close together. And if we zoomed in even further, each if those lines would be made up of several different lines, even closer together. There is actually an infinite level of detail within the image, you could zoom in forever and never get to the end.
We call this shape a strange attractor. Attractor because it appears to attract all the point to it, and strange because such a complex shape has been created from such a simple formula.
You can vary the values of the parameters to create different variants of the fractal. It will usually create a fractal of some type, but not all values will create pleasing images.
Drawing the fractal in generativepy
generativepy gives you several drawing options. For fractals like this one that involve setting individual pixels, the best way is to use the nparray module. This represents an image as a NumPy array, which allows you to access pixels very efficiently, as well as giving you lots of other useful processing options. The NumPy array is ultimately saved as a PNG image.
In this case we will use a greyscale NumPy array, which is an int array of dimensions height by width by 1. Each element is an integer value between 0 (black) and 255 (white).
Remember that NumPy stores elements in rows then columns, so the first value is the y coordinate (the row) an the second value is the x coordinate (the column). This also means that this size is expressed as height then width.
The code
Here is the full code of the fractal:
from generativepy.bitmap import Scaler
from generativepy.nparray import make_nparray
MAX_COUNT = 100000
A = 0.9
B = -0.6013
C = 2.0
D = 0.5
def paint(image, pixel_width, pixel_height, frame_no, frame_count):
scaler = Scaler(pixel_width, pixel_height, width=3, startx=-2, starty=-2)
x = 0.01
y = 0.01
for i in range(MAX_COUNT):
x, y = x*x - y*y + A*x + B*y, 2*x*y + C*x + D*y
px, py = scaler.user_to_device(x, y)
image[py, px] = 0
make_nparray('tinkerbell-bw.png', paint, 600, 600, channels=1)
We are using make_nparray to create the image, with a size of 600 by 600, and 1 channel (ie greyscale). This function calls our paint function, passing in a NumPy array that we can fill without pixel values. The array is prefilled with the value 255 (white). If we set any array value to 0, it will cause that pixel in the image to be black.
The Tinkerbell formula creates values that have x and y values between -2 and +1. In order to create a suitable image, we need to map these x and y values onto equivalent pixel positions in the range 0 to 599 (since our image is 600 pixels square). We use a Scaler to convert x and y values into pixel positions, using the user_to_device function.
In the main loop of the paint function, we loop 100,000 times, calculating new x and y values and setting the corresponding pixel to black. make_nparray then writes this array out as an image file tinkerbell-bw.png, which you can see at the start of this article.
Adding colour
The black and white image is a little boring. in the next article we will see how to add colour to make a more interesting image.
See also
Join the PythonInformer Newsletter
Sign up using this form to receive an email when new content is added:
Popular tags
2d arrays abstract data type alignment and angle animation arc array arrays bar chart bar style behavioural pattern bezier curve built-in function callable object chain circle classes clipping close closure cmyk colour combinations comparison operator comprehension context context manager conversion count creational pattern data science data types decorator design pattern device space dictionary drawing duck typing efficiency ellipse else encryption enumerate fill filter font font style for loop formula function function composition function plot functools game development generativepy tutorial generator geometry gif global variable gradient greyscale higher order function hsl html image image processing imagesurface immutable object in operator index inner function input installing iter iterable iterator itertools join l system lambda function latex len lerp line line plot line style linear gradient linspace list list comprehension logical operator lru_cache magic method mandelbrot mandelbrot set map marker style matplotlib monad mutability named parameter numeric python numpy object open operator optimisation optional parameter or pandas partial application path pattern permutations pie chart pil pillow polygon pong positional parameter print product programming paradigms programming techniques pure function python standard library radial gradient range recipes rectangle recursion reduce regular polygon repeat rgb rotation roundrect scaling scatter plot scipy sector segment sequence setup shape singleton slice slicing sound spirograph sprite square str stream string stroke structural pattern subpath symmetric encryption template tex text text metrics tinkerbell fractal transform translation transparency triangle truthy value tuple turtle unpacking user space vectorisation webserver website while loop zip zip_longest
