Numpy efficiency

When we talk about the efficiency of NumPy arrays (np arrays), what exactly do we mean? There are two separate issues:

• Efficiency of memory usage.
• Processing efficiency.

Why are NumPy arrays more efficient than Python lists?

The basic reason NumPy is more efficient is that it is written in C rather than Python. C is a very efficient language but it tends to be slightly more complicated to use than Python. So it generally takes longer to write the equivalent code in C rather than Python, but the code will then run faster.

NumPy gives us the best of both worlds. Someone else has done all the difficult work of coding the functions in C, then put it in a Python wrapper so we Python programmers can benefit.

C has two advantages. Firstly it is a compiled language. This means that after the code has been written, it is converted (compiled) into optimised machine code (the low-level language the CPU speaks) so it is blazing fast. Python, on the other hand, is an interpreted language, which means it is converted to machine code as it is executed, which will always be a bit slower. Also, the interpreter can't optimise that code in quite the same way that a C compiler can, because the compiler can spend more time and look at the whole program to find clever and devious speedups.

The second advantage is that C uses primitive data types. Things like ints, floats and booleans are stored directly in memory in the native format the CPU uses. In Python, everything is an object, so even simple integer values need extra steps before the CPU can work on them. Python objects also take more memory than primitive data values

Memory usage

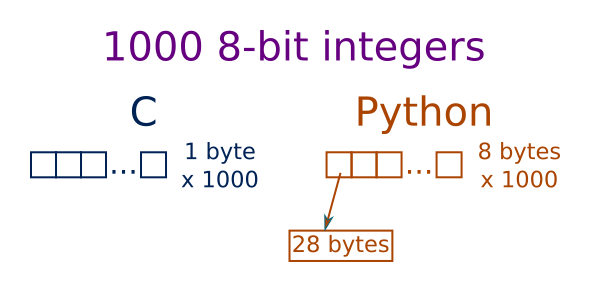
NumPy is written in C, which is quite a low-level language. Values are stored directly in memory. If you want to store an 8-bit integer using C, it takes exactly one byte.

In Python, numbers are stored as objects. Every Python object has to store information about its type, and also a reference count (to tell Python when the object is no longer being used, so it can be automatically deleted), in addition to the actual value of the object. The exact amount of memory used can depend on the type of computer you have (whether it is a 32-bit or 64-bit system) and which Python implementation you are using. On my 64-bit computer, it takes 28 bytes to store an 8-bit integer.

Now consider an array of 1,000 8-bit numbers. In C, the elements of an array are stored one after the other in a single block of memory. So an array of 1000 8-bit numbers takes exactly 1,000 bytes.

In Python, a list is an object, and each of its elements (the numbers) is another separate object. The list contains an array of references, which point to the element objects. On a 64-bit computer, each reference is 8 bytes long. With various other information the list has to store, the list object itself is a little over 8,000 bytes.

But don't forget, that is just the list! Each element of the list (each number) requires 28 bytes. So 1,000 elements take over 36,000 bytes of storage.

If you have a 2-dimensional array of 1000 by 1000 elements, again C stores these elements one after the other in a single block of memory. It stores the 1000 bytes of the first row, followed immediately by the 1000 bytes of the second row, etc. So the whole arrays takes exactly 1,000,000 bytes (1,000 x 1,000).

In Python, a 2D list is implemented as a list of lists. Each row is a separate list of 1000 elements (taking about 36,000 bytes). There are 1,000 of these lists, one for each row. There is also the main list, the list of all the rows - but with so many lists already, one extra doesn't make much difference to the total amount of space used. the total space used would be a little over 36,000,000 bytes.

Example of memory usage

A high-quality digital image of about 10 million pixels would require about 30 MBytes to store in a NumPy array but would take about a gigabyte to store as a standard Python list.

If you were writing an image editor, you might need to store several versions of the image in memory (for example, if you wanted to be able to undo the most recent changes), which would take several gigabytes. If you wanted to edit several images at the same time, you would need tens of gigabytes, which starts to get unmanageable. Using NumPy arrays requires a fraction of the memory.

Processing efficiency

Suppose we wanted to take an existing NumPy array a and use it to create a new NumPy array b, where each element of b is one greater than the corresponding element of a. That is, if a is:

[1, 3, 8, 0]

we would create b with elements:

[2, 4, 9, 1]

The code to do this is (assuming a contains a NumPy array):

b = a + 1

The whole process of looping over the values in a, adding 1 to each value, and storing the result in b, is executed in highly efficient C code in the NumPy library. Here is a diagram of what happens:

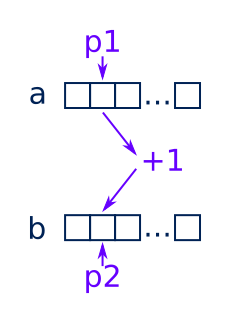
Arrays a and b are stored contiguously in separate areas of memory. A pointer p1 points to the current element in a, and p2 points to the current element in b. Here is what the main loop does (assuming n is the length of a):

1. Loop n times:
2. Read the value from memory location p1
3. Add 1 to the value
4. Store the new value in memory location p2
5. Increment p1
6. Increment p2

Each of these operations is very simple and might be performed by a single CPU instruction. The whole loop might take just a handful of instructions, and run very quickly indeed.

Now let's do the same thing with normal Python lists. The code would look like this:

b = []
for x in a:
    b.append(x+1)

or if you prefer to use list comprehensions:

b = [x + 1 for x in a]

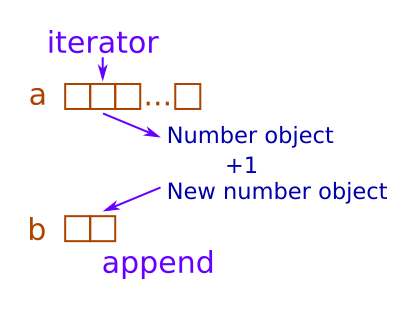
Here is what python needs to do to execute this loop:

1. Create an iterator to loop over a:
2. Get the next value of list a, and store it in integer x
3. Calculate x + 1 and create a new integer object
4. Append the value to b

This code isn't horribly inefficient, it will still run quite quickly. Python itself may optimise some of these steps. But it will be a lot slower than the highly optimised code in the NumPy library, for several reasons:

• It uses an iterator to get the values from a rather than a simple pointer.
• Values in the list are Python int objects, rather than simple byte values.
• Numbers in Python are immutable, so to add 1 to x a new number object must be created.
• The result has to be appended to list b rather than just written to a memory location.

This might take a few dozen instructions, rather than a handful that NumPy takes, and might run 10 times slower (of course, a lot depends on exactly what you are doing, what type of processor you are running on, and how much optimisation Python can perform).

Optimizing NumPy

To get the best performance from NumPy, there are a few things to bear in mind.

Choose the right data type depending on your application. Unlike Python, where there is only one type of integer and one type of float, NumPy has different types. For example, if you are processing image data you probably only need to store data values in the range 0 to 255. You can use the np.uint8 data type for that, which uses 1 byte per element. If you were to use a different data type, such as np.uint64, then it would use far more memory to store the same data (a uint64 uses 8 bytes).

Avoid explicit calculation loops, use universal functions and vectorisation instead. It will be much faster.

Try to avoid all loops as any kind of loop in NumPy will be slower than using NumPy special functions. Whatever you need to do, there will probably be a NumPy function to help you, and that will almost always be faster than a Python loop. See the indexing and advanced vectorisation sections.

See also

• Key advantages of NumPy
• Anatomy of a numpy array